When discussing black holes, the concepts of singularity and event horizon frequently dominate the conversation. Traditionally, these elements define black holes in the framework of general relativity. However, recent discussions among physicists suggest that black holes may not necessarily require singularities or even event horizons to exist.
To understand this debate, it’s crucial to differentiate between theoretical and observed black holes. Theoretical black holes stem from solutions to Einstein’s general relativity field equations, commonly referred to as metrics. The first of these, the Schwarzschild metric, was introduced by Karl Schwarzschild and describes a simple, non-rotating black hole. In 1963, Roy Kerr expanded this concept by developing the Kerr metric, which applies to rotating black holes and has inspired numerous visual representations in popular media, including the film *Interstellar*.
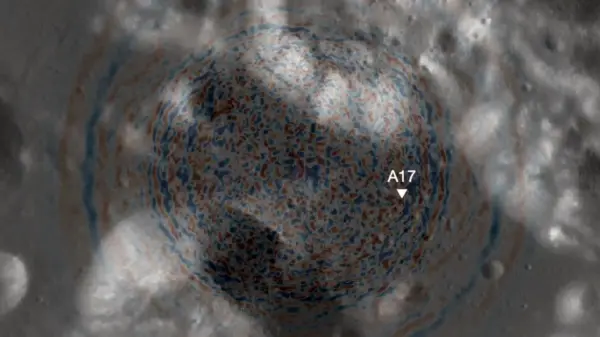
On the observational side, significant data collected by the Event Horizon Telescope has focused on black holes such as M87* and Sagittarius A*, the latter located at the center of our galaxy. These observations indicate that both black holes rotate and exhibit structures that align closely with the Kerr model. Yet, due to the inherent nature of black holes, direct observation of their interiors remains impossible, leaving the existence of singularities uncertain.
Understanding black holes is further complicated by the implications of singularities and event horizons. Singularities represent mathematical points of infinite density where the laws of physics cease to function coherently. Physicists have proposed the cosmic censorship hypothesis, suggesting that singularities must be concealed by event horizons to avoid these paradoxes. Nonetheless, event horizons pose their own set of challenges, particularly regarding the information paradox, which asserts that information falling into a black hole is irretrievably lost to the universe.
A potential solution to the complexities surrounding black holes lies in the exploration of models that do not incorporate singularities or event horizons. Considering that general relativity is a classical theory, the need arises for a quantum theory of gravity to address these phenomena. Evidence from quantum mechanics suggests that singularities might be prevented from forming altogether. For instance, the Heisenberg’s uncertainty principle implies that an exact mass cannot exist at a precise point, indicating that quantum mechanics could negate the conditions necessary for singularity formation. Furthermore, Hawking radiation could theoretically permit energy and information to escape a black hole over time.
Theoretical advancements in this area include models such as loop quantum gravity and string theory. Loop quantum gravity posits that the quantum foam of spacetime may lead to the formation of a “Planck star” rather than a singularity. Similarly, string theory introduces the concept of a fuzzball, replacing the singularity with a spherical configuration of degenerate strings.
In addition to these quantum models, alternative classical theories have emerged that aim to alleviate the issues inherent in general relativity. One such model is the Hayward metric, which represents a solution to Einstein’s field equations under specific constraints: it is static, asymptotically flat, spherically symmetric, and notably, non-singular. Unlike the Schwarzschild black hole, which adheres to the first three constraints, the Hayward model eliminates the singularity entirely.
The Hayward black hole features a locally flat center rather than a point of infinite density. Unlike traditional black holes, it does not possess an event horizon; instead, it has an apparent horizon that retains matter for an extended period, allowing for gradual escape of matter and energy. This mechanism appears similar to Hawking radiation but operates independently of quantum physics. For supermassive black holes, the differences between the Hayward and Schwarzschild models are minute, making them nearly indistinguishable in practice.
While current observations of black holes consistently align with established models, Hayward black holes also fit the available data. Nonetheless, a significant caveat remains: no known physical mechanism currently exists to prevent singularities from forming, as the Hayward model inherently assumes their exclusion. If the Hayward model holds true, it could render the traditional problems associated with singularities and event horizons irrelevant.
As the scientific community continues to investigate these theories, it emphasizes the importance of exploring new models in the quest to understand the complexities of black holes. The implications of these discussions not only deepen our knowledge of the universe but also challenge long-standing assumptions about the very nature of black holes.